“Compound Interest is the Eighth Wonder of the World.”
– Albert Einstein
To begin the journey of financial independence understanding the key concept of compounding (sometimes referred to as exponential growth of compound interest) is vital.
There is a parable known as the wheat and checkerboard problem. It starts out with 64 squares on a checkerboard and the grains of wheat double on each successive square such as one grain (square 1) + two grains (square 2)+ 4 grains (square 3) and so forth for all 64 squares.
The total number of grains will grow to 18,446,744,073,709,551,615 (eighteen quintillion, four hundred forty-six quadrillion, seven hundred forty-four trillion, seventy-three billion, seven hundred nine million, five hundred fifty-one thousand, six hundred and fifteen). This staggering number would be equivalent to over 1.4 trillion metric tons of wheat which is over 2,000 times the annual worldwide production of wheat. This helps illustrate the power of exponential growth or compounding.
With that in mind, it can also help with learning amount the concept of the time value of money. Over a long time frame of 20, 30, 40, 50 years a fairly modest amount of dollars contributed can grow to significant value to help achieve financial independence. Let’s look at some examples.
Saving and investing over time should have the benefit of the time value of money and the power of compounding. In the image below, an initial contribution of $2,000 is made with an additional $100 added monthly. At an 8% annual rate of return, these contributions may increase to nearly $545,000 over 45 years. The total amount contributed was $56,000 which was the $2,000 initial contribution and the monthly $100 contribution. At the 8% rate of return over the 45 years of growth (which could be from age 20 to age 65), the amount of growth, or earnings, is $489,000. The graph shows how the contributions remain fairly modest over time and how the total amount continues to grow exponentially over time.
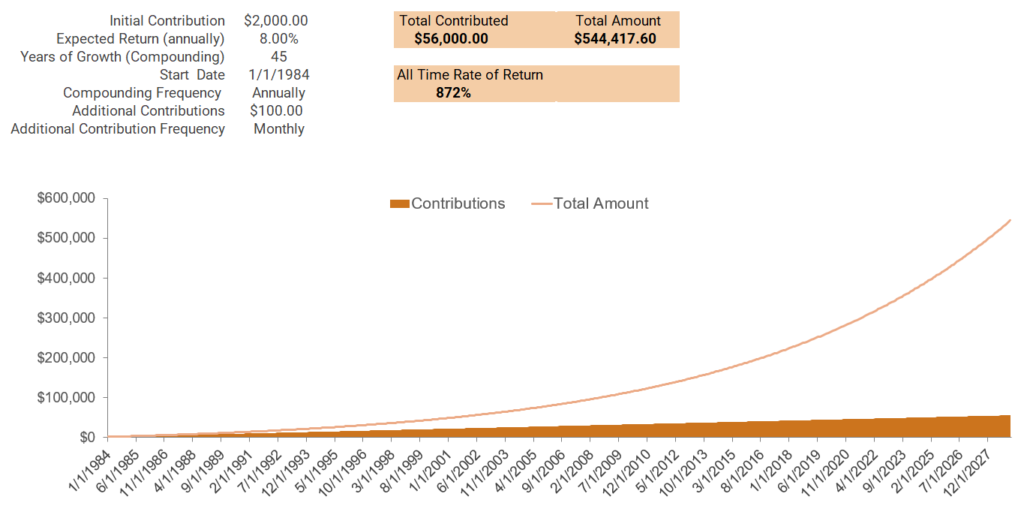
This example clearly demonstrates that power of compounding with the assumption that $2,000 was initially contributed into some investment that grew at 8% annually with an additional $1,200 contributed yearly at $100 per month. The main takeaway and lesson is to start trying to save early and often.
In this next example, we will look at two people, Joe and Jane. In this example, Jane decides to contribute $4,000 per year over ten years from age 22 to age 31. The contributions grow at an 8% annual rate of return. After age 31, Jane does not make any additional contributions beyond the $40,000 contributed over 10 years. At age 67, the amount invested at an 8% annual rate of return could grow to just shy of $1,000,000, $999,319 to be exact.
| 8% | Jane | Joe | Joe | |||||
| Age | Contribution | Growth | Contribution | Growth | Contribution | Growth | ||
| 22 | $4,000 | $4,320 | $0 | $0 | $0 | $0 | ||
| 23 | $4,000 | $8,986 | $0 | $0 | $0 | $0 | ||
| 24 | $4,000 | $14,024 | $0 | $0 | $0 | $0 | ||
| 25 | $4,000 | $19,466 | $0 | $0 | $0 | $0 | ||
| 26 | $4,000 | $25,344 | $0 | $0 | $0 | $0 | ||
| 27 | $4,000 | $31,691 | $0 | $0 | $0 | $0 | ||
| 28 | $4,000 | $38,547 | $0 | $0 | $0 | $0 | ||
| 29 | $4,000 | $45,950 | $0 | $0 | $0 | $0 | ||
| 30 | $4,000 | $53,946 | $0 | $0 | $0 | $0 | ||
| 31 | $4,000 | $62,582 | $0 | $0 | $0 | $0 | ||
| 32 | $0 | $67,589 | $4,000 | $4,320 | $4,949 | $5,345 | ||
| 33 | $0 | $72,996 | $4,000 | $8,986 | $4,949 | $11,117 | ||
| 34 | $0 | $78,835 | $4,000 | $14,024 | $4,949 | $17,351 | ||
| 35 | $0 | $85,142 | $4,000 | $19,466 | $4,949 | $24,084 | ||
| 36 | $0 | $91,953 | $4,000 | $25,344 | $4,949 | $31,355 | ||
| 37 | $0 | $99,310 | $4,000 | $31,691 | $4,949 | $39,208 | ||
| 38 | $0 | $107,254 | $4,000 | $38,547 | $4,949 | $47,689 | ||
| 39 | $0 | $115,835 | $4,000 | $45,950 | $4,949 | $56,849 | ||
| 40 | $0 | $125,102 | $4,000 | $53,946 | $4,949 | $66,742 | ||
| 41 | $0 | $135,110 | $4,000 | $62,582 | $4,949 | $77,426 | ||
| 42 | $0 | $145,919 | $4,000 | $71,909 | $4,949 | $88,965 | ||
| 43 | $0 | $157,592 | $4,000 | $81,981 | $4,949 | $101,427 | ||
| 44 | $0 | $170,199 | $4,000 | $92,860 | $4,949 | $114,885 | ||
| 45 | $0 | $183,815 | $4,000 | $104,608 | $4,949 | $129,421 | ||
| 46 | $0 | $198,521 | $4,000 | $117,297 | $4,949 | $145,119 | ||
| 47 | $0 | $214,402 | $4,000 | $131,001 | $4,949 | $162,073 | ||
| 48 | $0 | $231,554 | $4,000 | $145,801 | $4,949 | $180,384 | ||
| 49 | $0 | $250,079 | $4,000 | $161,785 | $4,949 | $200,159 | ||
| 50 | $0 | $270,085 | $4,000 | $179,048 | $4,949 | $221,517 | ||
| 51 | $0 | $291,692 | $4,000 | $197,692 | $4,949 | $244,583 | ||
| 52 | $0 | $315,027 | $4,000 | $217,827 | $4,949 | $269,494 | ||
| 53 | $0 | $340,229 | $4,000 | $239,573 | $4,949 | $296,398 | ||
| 54 | $0 | $367,448 | $4,000 | $263,059 | $4,949 | $325,455 | ||
| 55 | $0 | $396,843 | $4,000 | $288,424 | $4,949 | $356,836 | ||
| 56 | $0 | $428,591 | $4,000 | $315,818 | $4,949 | $390,727 | ||
| 57 | $0 | $462,878 | $4,000 | $345,403 | $4,949 | $427,330 | ||
| 58 | $0 | $499,908 | $4,000 | $377,355 | $4,949 | $466,861 | ||
| 59 | $0 | $539,901 | $4,000 | $411,864 | $4,949 | $509,555 | ||
| 60 | $0 | $583,093 | $4,000 | $449,133 | $4,949 | $555,664 | ||
| 61 | $0 | $629,741 | $4,000 | $489,383 | $4,949 | $605,462 | ||
| 62 | $0 | $680,120 | $4,000 | $532,854 | $4,949 | $659,243 | ||
| 63 | $0 | $734,530 | $4,000 | $579,802 | $4,949 | $717,328 | ||
| 64 | $0 | $793,292 | $4,000 | $630,507 | $4,949 | $780,058 | ||
| 65 | $0 | $856,755 | $4,000 | $685,267 | $4,949 | $847,808 | ||
| 66 | $0 | $925,296 | $4,000 | $744,409 | $4,949 | $920,977 | ||
| 67 | $0 | $999,319 | $4,000 | $808,281 | $4,949 | $1,000,000 | ||
| $40,000 | $144,000 | $178,156 |
On the other hand, Joe does not make any contributions during the first 10 years from age 22 to age 31. Starting at age 32, Joe decides to contribute $4,000 each year from age 32 to age 67. Despite total contributions of $144,000 over that timeframe, Joe’s nest egg will have approximately $800,000, $808,281 to be exact. As the time value of money was less on Joe’s side his investment was overshadowed by Jane’s by nearly $200,000. Although a bit long and possibly difficult to read, the table below provides the year by year growth for Jane and Joe from age 22 to age 67.
Often time, a “what if” scenario may be looked at to best understand the time value of money to achieve a goal. Let’s say that at age 32 when Joe decides to start contributing more earnestly to his savings, how much would he need to contribute monthly to have $1,000,000 savings at an 8% annual growth rate?
The two right columns at the table above illustrate that Joe would need to contribute nearly $5,000 per month, $4,949 to be exact, for his savings to have the opportunity to grow to $1,000,000 by age 67.
In the example, Joe started 10 years later than Jane. Jane stopped after 10 years and contributed $40,000 to grow towards $1,000,000. Joe had to contribute $178,156 at $4,949 monthly to achieve the same financial goal. Here again, this demonstrates in a very realistic way the concept of the time value of money and power of compounding.
The main takeaway is demonstrated in a convincing manner to save early and often. Fairly modest amounts saved have the potential to grow significantly over 20, 30, 40 or 50 or more years. In doing so, you greatly improve you potential to achieve financial independence.

Focus on long term savings with the power of compounding
Leave a Reply